
 Share This Page
Share This Page| Home | | Ham Radio | |  |  |  Share This Page Share This Page |
 Morse Code
Morse Code
A treatise on an old, very reliable communication method
— All content Copyright © 2017, P. Lutus — Message Page —
Version 1.9 2024.05.04
(double-click any word to see its definition)
Morse code — dots and dashes — heralded the dawn of radio and of wireless communication. There were many reasons for the use of Morse code at that time, one being that the primitive technology imposed severe limitations on the kinds of information that could be impressed on a radio signal. Guglielmo Marconi achieved the first transatlantic radio communication with a crude spark gap transmitter, before vacuum tubes were commonly available. Because the signal was readable Morse code, the eager listening team in Newfoundland knew they were hearing something other than lightning.
Imagine that you're listening to faint and crude radio signals from across the Atlantic ocean in the time of Marconi's pioneering work — for a Morse code sample, click here:

Now imagine you're a radio operator on a ship in the North Atlantic on April 15th 1912, and you hear a faint radio signal from somewhere in the darkness — click this example to hear how it might have sounded:

As technology improved, so did long-distance radio communications. Once vacuum tube transmitters with quartz crystal signal sources replaced spark gap transmitters, much clearer transmissions over greater distances became possible. By the time I became a ham radio operator in the 1950s, radiotelegraphy had become more consistent and reliable — click this example:

The above Morse code means "Calling any distant (DX) stations, this is ham radio operator KE7ZZ calling and listening."
From a modern perspective Morse code has a number of drawbacks including a data rate much slower than voice or modern digital methods, but over long distances, in adverse conditions or with little transmitter power available, it has been the preferred mode for reliable point-to-point communications — until recently.
In 2007 the (U.S.) Federal Communications Commission dropped the requirement that ham radio operators be able to send and receive Morse code (similar changes have taken place in commercial and military radio operations). Many celebrated this change for a number of reasons — modern wireless communications no longer relies on Morse, even over long distances and critical applications, and the requirement was stopping many people from getting ham radio licenses and starting an interesting hobby.
From my perspective, now that Morse is a dead art, my interest has increased — sort of like wanting to learn Latin on realizing no one speaks it any more. This page is dedicated to the lost art of Morse code, which is able to communicate more information over greater distances, in the presence of poorer atmospheric conditions and interfering signals, than any other method.
In this section, users can translate sample text into Morse code, or paste their own text into the practice window and translate that. This editing feature lets you create custom code while learning to listen to and decode Morse.
To use this feature, just click the provided link to translate the default text sample, or if you prefer, click below to erase the default text sample, type or paste your own text into the practice window, then click the Start button to start/stop translation.
This section allows the user to make and save a recording of the Morse code generated above. To use this feature:
- Click the "Enable Audio Recording" checkbox below.
- Operate any of the Morse generator functions on this page.
- Return here to play and/or save the result.
- If this feature doesn't work on your browser (i.e. any Microsoft browser), well ... change browsers. At the time of writing, neither of Microsoft's browsers supports this feature, but both Google Chrome and Firefox do.
To save a recording, right-click the play arrow and choose "Save audio as ..." or another available feature.
Remember to disable the recording feature when you're done — it uses browser memory when enabled.
This section allows users to listen to a sequence of Morse code audio signals and type the corresponding characters on the computer keyboard. This is an efficient way to learn how to translate Morse code into text. The user may choose which subsets of Morse code are included — letters, numbers, and different punctuation sets:
- Letters (a-z)
- Numbers (0-9)
- Common Punctuation ()
- Exotic Punctuation ()
Press "Start" below, then type a guess about the Morse character you hear. If your guess is correct, a new character will be generated. If there's an error, the program will beep and repeat the missed character. Press "Stop" to end the practice session.
... Use the Control Panel below to change the code practice transmission rate and other properties.
This panel allows fine tuning of the Morse code generator's values. Simply change a setting at the right and generate some code to hear the result. Your changes are saved in a browser cookie for later use. A full explanation of the values appears below the entry panel.
Note: For an immediate change, press Enter after making your entry.

Figure 1: Code timing diagram
Explanation:
Dot constant. We compute the time duration of a Morse code dot using this equation:
\begin{equation} dd = \frac{dc}{wpm} \end{equation}
Where:
- dd = Duration for one dot, units seconds.
- dc = Dot Constant.
- wpm = Desired words per minute.
The value dc is set by convention to 1.2 (units seconds) as explained here. This value produces code timings that differ slightly from that of the ARRL code practice recordings, which many people consider an excellent resource. Users are free to choose a different value for this quantity, which will be saved between sessions.
NOTE: Each of the dot times listed below is added to the prior value. So an entered value of 2 for dot time between characters produces an effective dot time of 3 (2+1). In the same way, an entry of 4 for dot time between words produces an effective dot time of 7 (4+2+1) — see Figure 1.
Dot time between dots and dashes. Scaled by dd as in equation (1). This is the duration of the silent pause between any two dots or dashes within a Morse code element, and the value is proportional to a dot duration.
Dot time between characters. Scaled by dd as in equation (1). In much the same way, this entry determines the duration of the pause between complete Morse code elements.
This value also plays a part in the Farnsworth speed method described below.
Dot time between words. Scaled by dd as in equation (1). This entry determines the duration of the pause between entire words of code.
This value can be used to stretch the interval between words while maintaining a specific WPM rate for the individual Morse code elements. This entry (and the dot time between characters entry above) allows creation of Farnsworth-speed code, popular for teaching Morse. The Farnsworth scheme creates a difference between character speed and text speed, which allows the student to hear individual characters at a relatively high rate, but allows more time between characters and words for interpretation.
Speed WPM. Units words per minute. In connection with the Dot Constant and equation (1) above, this entry determines the overall speed of the code.
Frequency. Units Hertz. The pitch of the generated code. A frequency entry of 0 will produce a DC level at the computer's audio output, suitable for operating a relay or other device to be time-synchronized with the Morse code's dots and dashes.
- Volume. A value of 1.0 represents full volume. Values greater than 1.0 will produce distortion in the computer's audio output.
Slope Constant. Units seconds. This value determines the waveform rise and fall time for the generated dots and dashes. To understand the reason for this setting, try setting it to zero and see how the code sounds. This rise and fall time issue is particularly important in radio communication because an improperly designed transmitter, one with rapid rise and fall times, creates sidebands much wider than necessary and interferes with other transmissions. The default value is 0.005 (5 milliseconds).
Scope Timing Trace
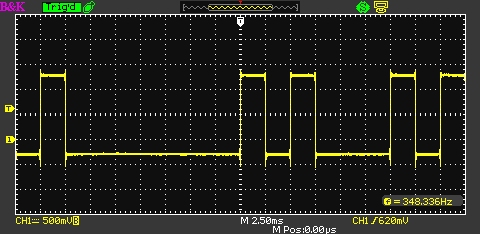
Figure 2: Oscilloscope trace for repeated letter "i" ("..").
Figure 2 captures this page's Morse generator output with a frequency setting of 0 (which produces a DC level at the computer's audio output, convenient for oscilloscope measurements). The center of the display is the beginning of the letter "i" (".."). The first dot is followed by one dot-time, then another dot, then an intercharacter pause of 3 dot times. At the left center of the display is the inter-word pause of 7 dot times after the prior word.
Here's a list of widely accepted Morse code sequences. Click the characters to hear them rendered as Morse code.
All my programs are released under the GPL, which means you can use them in your own projects, adapt the code to your own purposes, as long as my copyright notices are preserved in the source listings.
This Web page uses JavaScript to generate Morse code — click here to see/download the source.
- I have also written a Java Morse code generator — click here to download the JAR file. To use the Java program, install Java if you haven't already, then open a command prompt in the same directory as the JAR file and enter:
Some helpful text will appear. To translate some code:$ java -jar morse_sender.jar$ java -jar morse_sender.jar here is my textThere are a number of other ways to supply the text to be translated, as shown in the help screen.
Click here to view/download the Java source.
- I have written a Python code generator also, which operates very much like the Java program — click here to view/download the program listing. Much like the Java program, make sure you have Python 3 installed on your system and open a command shell:
$ ./morse_sender.py (for help) $ ./morse_sender.py here is my textThe above might not work so well on Windows unless Python has been installed in a way that makes it visible everywhere on your system.
Land Telegraphy
Although Morse code saw its greatest use in connection with radio, it came into existence before radio even existed. Samuel F. B. Morse co-created the first version of Morse Code in the early 19th century while developing and pioneering the use of land telegraph systems.
In those times, when the sender pressed a telegraph key, the "receiver" — an electromagnetic relay — would close: clack! Compared to the ease of understanding modern code tones transmitted by radio, I imagine it required some practice to distinguish dots from dashes and signals from silence, while listening to a chattering relay.
Required Bandwidth
Radiotelegraphy signals require very little bandwidth, and many more code transmitters can be crowded into a given band than when using other radio schemes. The explanation has to do with the relationship between information content and bandwidth — more information in a given time interval, more bandwidth required. This relationship is formally defined as the Nyquist frequency theorem, which briefly says that to support the transmission of N bits per second of information, the information channel must have a bandwidth of 2N.
Consider this relationship between different radio modulation methods:
Mode Bandwidth Required Morse code (CW) 100 Hz Single sideband (SSB) 5 KHz Amplitude Modulation (AM) (broadcast) 10 KHz Frequency Modulation (FM) (broadcast) 100 KHz HDTV (broadcast, compressed) 8-16 MHz Data Rate
Another way to look at this is to compare the time required to transmit a book-length manuscript, by comparing Morse code with other wireless methods. A typical modern book has 70,000 words, each word an average of five characters, so 350,000 characters.
If we transmit the book's words by Morse code at 13 five-character words per minute, and disregarding data lost to missing punctuation and uppercase-only alphabetic characters, and assuming a continuous effort with no breaks for darkness or fatigue, we would need almost 90 hours or 3.74 days.
How much time would a book recital require? A professional speaker can produce a word rate of 155 words per minute, so — again without any pauses for fatigue or bathroom breaks — we would need 7.5 hours.
Skipping over digital television and other difficult-to-quantify transmission methods, let's see how much time would be required to transmit the book in digital form, using a modern wireless channel. I chose 802.11g for this example, to avoid the science fiction element inherent in the newer, faster protocols. The 802.11g maximum data rate is 54Mbps (megabits per second), which can be converted to 6.75 MBps (megabytes per second) if we assume eight bits per byte. Using this communication method, the book can be transmitted in ... wait for it ... about ten milliseconds or 1/100 of a second.
The takeaway? It requires roughly 31 million times longer to transmit the book by Morse code than with modern methods.
QRP
The code phrase QRP means using the minimum amount of power required to communicate. Because Morse code requires such a small bandwidth, it follows that a receiver can be adjusted to accept only a small bandwidth that includes the desired signal. This adjustment greatly reduces interference from noise sources and other transmitters, which means a very small transmitter power can be used. Even though U.S. radio amateurs can use as much as 1000 watts of transmitter power, those who choose to use the smallest amount of power can easily accomplish their communications with five watts or less — by using Morse code.
Using specialized receiving methods, in experiments I've extracted a signal from a noise environment that was 100 times stronger (+40db). In my phase-locked-loop article I describe the method in detail and include example code. This means if I knew which frequency to monitor and using the phase-locked-loop method, I could receive a signal from a small transmitter on Mars. This idea would only work if the participants used Morse code.
Thanks for reading!
Exclamation point Error
| Home | | Ham Radio | |  |  |  Share This Page Share This Page |