
 Share This Page
Share This Page| Home | | Articles | |  |  Share This Page Share This Page |

In "Infinity War", Marvel Comics super-villain Thanos kills off half the world's population. Would this fix the planet?
— P. Lutus — Message Page —
Copyright © 2019, P. Lutus
Most recent update:
(double-click any word to see its definition)
First, I think it's encouraging that movies like "Avengers: Infinity War" focus on environmental and population issues — it means people understand and accept the idea that we face serious problems caused by overpopulation. That's a good thing. The fact that people understand the movie's premise means we know that pollution, climate change, disease epidemics, crime and other issues aren't independent problems — they're all symptoms of an underlying problem: world overpopulation.
To answer the title question, for reasons given here the Thanos "solution" couldn't work, but there's a much better solution in reality. In this article I explain why Thanos was wrong, and how we can solve the problem in a much better way.
Supervillain Thanos' big idea is to make half the world's people disappear ("But at random, dispassionate, fair to rich and poor alike"), in a supernatural weeding out process. Why wouldn't this work?
Rate of Population Increase
Thanos' strategy would fail because of the speed at which world population increases. Let's say population increases by 1% per year (it's faster than this, but bear with me). Let's start with a naive conclusion: with a 1% per year increase, it would take 100 years to double the world's population:
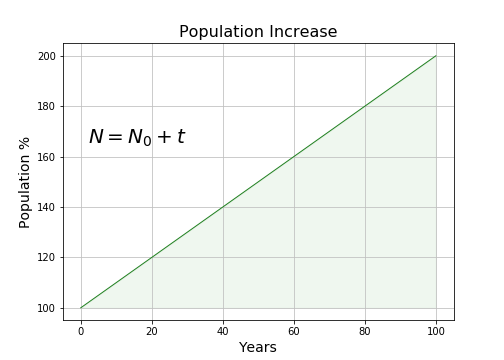
Chart 1: Simple Increase
But this analysis overlooks something: children bear their own children and this amplifies the rate of increase. So the real growth rate is sort of like compound interest in a bank account — world population increases faster than we might expect:
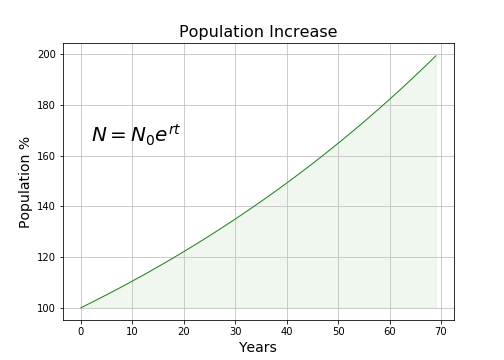
Chart 2: Exponential Increase
So with a 1% growth rate, it would take only 69 years to double the world's population. But a 1% increase is a bit too low — the actual (2019) population growth rate is 1.08% per year, which doubles world population in just 64 years. This means the Thanos remedy would have no long-term effect — after 64 years, it would be just as though Thanos hadn't snapped his fingers.
Sustainability
Even if world population suddenly stabilized at its present level, we would still face serious problems — climate change, environmental destruction, loss of plant and animal species, and exhaustion of non-renewable resources. In fact, because of how fast we're depleting non-renewable resources, we can't even sustain our present population in the long term. Some sources suggest that Earth can sustain a long-term world population of about 2 billion people, about 27% of the present population (which is 7.7 billion people at the time of writing).
Logistic Equation
The above graphs assume infinite resources, but a more realistic model takes environmental limitations into account. The Logistic Equation, widely used in population studies, shows what happens when a population exceeds the carrying capacity of its environment. Here's an example: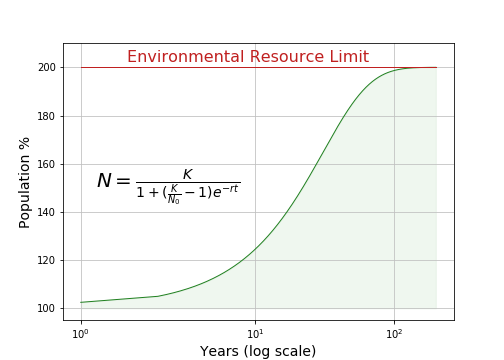
Chart 3: Logistic Model
In this realistic model, a population cannot exceed an environment's ability to sustain it. Once a population reaches the environment's natural limits (Chart 3, upper right), there can be no further growth, and deaths equal births.
Thanos Snaps his Fingers
To see the effect Thanos' "solution" would have, watch this short video:
Chart 4: The Snap
This shows why, in the long term, a population's rate of change is much more important than the total population at any paticular time.
A Two-Part Problem
To summarize the points made in this section, the population problem has two parts:
- The number of people.
- The rate of change in that number.
It does no good to address the population total and ignore its rate of change, which is why the Thanos solution wouldn't work. But there are methods that can work, if we have the courage to implement them.
Choice
Studies show that, when women are educated and given the right to choose, they have smaller families and their children are healthier and better educated as well:
Unesco: Education Leads to Smaller Healthier Families: "Educated women are more likely to use modern methods of contraception, and they tend to marry later. Educated parents of both sexes also generally desire smaller families than those with less education, and educated women tend to act on that reproductive preference for fewer children. In other words, women with more schooling are more likely to have the number of children they say they want."This section's take-away is that women must be provided with education and reproductive self-determination. No number of international environmental meetings and smoke-filled rooms can possibly equal the effect of giving women access to education, civil rights, and most important, the inalienable right to choose whether and when to have children.
Readers may ask, if this idea is so self-evident, why isn't it true already? The real reason isn't because educated women exercising reproductive choice is immoral as some would have you believe, it's because freedom of choice slows population growth, which slows economic growth, which causes rich people's stock holdings to stagnate in value. This is why many wealthy people fight so vigorously against freedom of choice — but not against their own daughters, only against poor people, tomorrow's cheap unskilled labor pool (more here).
But this will change. When world population stabilizes (charts 3 and 4 above), when it doesn't grow out of control as it's doing now, our entire economic system will have to change. A stock will increase in value only because a company becomes more efficient or innovative than its competitors, not just because every year there are more customers available to buy the same old products.
Diversity
Wouldn't a stable world population become genetically stagnant? Not if diversity is accepted and encouraged. And diversity isn't a mere fad, it's a core biological principle.
Human history can be seen as a dismal record of all the wrong ideas intended to solve population problems. If there's a central theme to this litany of grief, it's the intellectually bankrupt idea that there are good and bad people, and the world's problems can be solved by killing all the "bad" people. This is completely wrong, but not for the reasons we might think. It's not wrong because it contradicts civilized values, but because it contradicts biology.
In biology, the healthiest offspring arise from a mixing of genes from different sources, and the worst outcomes result from a failure to mix diverse genetic lines:
Genetic diversity: "... serves as a way for populations to adapt to changing environments. With more variation, it is more likely that some individuals in a population will possess variations of alleles that are suited for the environment. Those individuals are more likely to survive to produce offspring bearing that allele. The population will continue for more generations because of the success of these individuals."In the simplest terms:
- A family that limits mating to its own members is quickly destroyed — inbreeding: "... results in homozygosity, which can increase the chances of offspring being affected by deleterious or recessive traits. This usually leads to at least temporarily decreased biological fitness of a population (called inbreeding depression), which is its ability to survive and reproduce."
- The genetic principle that applies to families, applies equally to races, which is why the term "white supremacy" is an oxymoron.
Population Paradox
The Population Paradox arises when educated, conscientious men and women react to the fraught state of the world by choosing to have fewer or no children. Here's a recent example:
#nofuturenochildren: Hundreds of young people are pledging not to have children for the environment: "As leaders across the world are getting ready to gather together to discuss climate change — and what to do about it — at the UN Climate Change Summit in New York next week, hundreds of young people across the world are going on birth strike to pressure policymakers into action."Isn't this a good thing? Isn't this what we need? Well, looked at one way, yes — it is. But it leads to the Population Paradox, in which conscientious, socially aware people choose not to have children, while others, perhaps less interested in the state of the world, don't make this choice, which (assuming there are any genetic links to this behavior) may lead to more uncaring, uninvolved people in the future. Although real, this paradox can't be used to justify discriminatory choices or actions, it can only argue for an increase in educational opportunities for everyone.
Choice Means Choice
I want to emphasize that the availability of reproductive choice doesn't mean people must decide not to have children (that would contradict the meaning of "choice"), it means people must be free to choose, based on an educated grasp of the world they live in, an enlightened self-interest, and their right to choose. Any pressure or coercion, anything other than informed consent, really would be immoral.
That is precisely why the present system is immoral. By depriving young men and women of both education and choice, society is deciding for them, overruling the choices they would make if they had the required education, as well as the ability and right to make informed decisions.
Top-down versus Bottom-up
Most historical population control measures have been "top-down," either an oppressive regime that tried to exterminate one group and favor another, or a religion that tried to portray the most personal kind of choice as a moral obligation or a sin of omission.
It's my hope that the future will create a "bottom-up" alternative, in which an education in logic, mathematics and science will provide the kind of insight that will help individuals understand the meaning of their personal choices, and act accordingly.
Cost of Education
Ironically, at a time when education is increasingly important, the cost of education is rising faster than nearly any other household expense — this Forbes article reports that college costs are rising eight times faster than wages, and student loans represent the largest category of non-household debt.
There's nothing inherently expensive about education. Textbooks don't need to be as expensive as they are, and selling colleges to students has become a sleazy and unethical enterprise, not unlike selling used cars. The college-insider who wrote this article says, "The markup on college tuition is astronomically higher than the markup on a car" and "Moral hazard has run amok in the college system." This article reveals that the cost of a college education has risen 1,200 percent over 30 years, "far outpacing any other price the government tracks: food, housing, cars, gasoline, TVs, you name it.". If this isn't criminal, it should be.
Author H. G. Wells said, "Civilization is in a race between education and catastrophe." This is certainly more true now than when Wells said it in 1922, when world population was about 2 billion people. But as things stand, only the wealthiest people can afford higher education — an education that should be available to all, except that colleges have been taken over by greedy marketers.
The content in the main article shows that one cannot understand population without understanding mathematics, and it shows why most people who understand mathematics knew right away that the Thanos solution couldn't work. This section provides the math behind those results.
Population Modeling
Here is the key population equation:
\begin{equation} \displaystyle \log\left(\frac{N}{N_{0}}\right) = r t \end{equation} Where:
- $N_0$ = Population at time zero.
- $N$ = Population at time t.
- $r$ = Rate of population increase per period (1% = 0.01).
- $t$ = time in consistent units.
The term $r$ is called the Malthusian Parameter. In population studies, $r$ equals births minus deaths.
Source: Wolfram Math World: Population Growth
Derivative Forms
Because equation (1) is simple and well-behaved, all its derivative forms are easily acquired:
Future Population $N$:
\begin{equation} \displaystyle N = N_{0} e^{\left(r t\right)} \end{equation}Present Population $N_0$:
\begin{equation} \displaystyle N_0 = N e^{\left(-r t\right)} \end{equation}Time $t$:
\begin{equation} \displaystyle t = \frac{\log\left(\frac{N}{N_{0}}\right)}{r} \end{equation}Rate $r$:
\begin{equation} \displaystyle r = \frac{\log\left(\frac{N}{N_{0}}\right)}{t} \end{equation}In these equations $\log(x)$ refers to the natural logarithm, not the more common $\log_{10}(x)$ seen on many calculators. $e$, the base of natural logarithms, appears in equations (2) and (3) and is equal to:
\begin{equation} \displaystyle e = \lim_{n \to \infty} \left(1 + \frac{1}{n} \right)^n \end{equation}Doubling-time Table
One may use these equations in a variety of practical ways. For example, to compute the population doubling time for a given growth rate $r$, use this form: \begin{equation} \displaystyle t = \frac{\log(2)}{r} \end{equation}Here are some results from equation (7) (remember that 1% = 0.01):
Rate per annum % Doubling time years 1.00 69.31 1.14 60.65 1.29 53.91 1.43 48.52 1.57 44.11 1.71 40.43 1.86 37.32 2.00 34.66 2.14 32.35 In case the last table result seems unrealistic, according to this reference that was roughly the 1970 world population growth rate.
Remember about the above equations that they assume infinite resources and don't accommodate environmental constraints. Read on for a more realistic equation that deals with natural limits.
Logistic Equation
In biology, populations are often modeled using a more sophisticated equation that takes into account natural limits — the environment's carrying capacity. The Logistic Equation takes many forms, but all have in common the idea that a population can only increase until the environment no longer sustains it. Here is a typical form: \begin{equation} N = \frac{K}{1+\left(\frac{K}{N_0}-1\right) e^{-rt}} \end{equation} This equation adds one more term to the earlier parameters:
- $K$ = the carrying capacity of the environment.
Once the population reaches $K$ and as shown in Charts 3 and 4 above, there can be no further growth and deaths equal births.
| Home | | Articles | |  |  Share This Page Share This Page |